Skip to main content

Phonon dispersion

In Quantum Espresso, phonon dispersion is calculated using ph.x program, which is implementation of density functional perturbation theory (DFPT).

Here are the steps for calculating phonon dispersion:

(1) perform SCF calculation using pw.x

src/GaAs-phonon/pw.scf.GaAs.in
&control
  calculation = 'scf'
  prefix = 'GaAs'
  pseudo_dir = '../pseudos/'
  outdir = './tmp/'
  verbosity = 'high'
  wf_collect = .true.
/

&system
  ibrav = 2
  celldm(1) = 10.861462
  nat = 2
  ntyp = 2
  ecutwfc = 80
  ecutrho = 640
/

&electrons
  mixing_mode = 'plain'
  mixing_beta = 0.7
  conv_thr = 1.0e-8
/

ATOMIC_SPECIES
  Ga 69.723    Ga.pbe-dn-kjpaw_psl.1.0.0.UPF
  As 74.921595 As.nc.z_15.oncvpsp3.dojo.v4-std.upf

ATOMIC_POSITIONS
  Ga 0.00 0.00 0.00
  As 0.25 0.25 0.25

K_POINTS {automatic}
  8 8 8 0 0 0

We perform the SCF calculation:

mpirun -np 4 pw.x -i pw.scf.GaAs.in > pw.scf.GaAs.out
info

  1. Usually higher energy cutoff values are used for phonon calculation to get better accuracy.

  2. In case of two dimensional systems, use assume_isolated = '2D' in the SYSTEM namelist to avoid negative or imaginary acoustic frequencies near Γ\Gamma point. Read more here.

(2) calculate the dynamical matrix on a uniform mesh of q-points using ph.x

src/GaAs-phonon/ph.GaAs.in
&INPUTPH
  outdir = './tmp/'
  prefix = 'GaAs'
  tr2_ph = 1d-14
  ldisp = .true.
!  recover = .true.
  nq1 = 6
  nq2 = 6
  nq3 = 6
  fildyn = 'GaAs.dyn'
/

Run the calculation:

mpirun -np 4 ph.x -i ph.GaAs.in > ph.GaAs.out

The above calculation is computationally demanding. Our example calculation took about a whole day on a 2.6 GHz quad core processor.

info

You can restart an interrupted ph.x calculation with recover = .true. in the INPUTPH namelist. You can cleanly exit an ongoing calculation by creating an empty file with name {prefix}.EXIT.

(3) perform inverse Fourier transform of the dynamical matrix to obtain inverse Fourier components in real space using q2r.x. Below is our input file:

src/GaAs-phonon/q2r.GaAs.in
&INPUT
  fildyn = 'GaAs.dyn'
  zasr = 'crystal'
  flfrc = 'GaAs.fc'
/
mpirun -np 4 q2r.x -i q2r.GaAs.in > q2r.GaAs.out

(4) Finally, perform Fourier transformation of the real space components to get the dynamical matrix at any q by using matdyn.x.

src/GaAs-phonon/matdyn.GaAs.in
&INPUT
  asr = 'crystal'
  flfrc = 'GaAs.fc'
  flfrq = 'GaAs.freq'
  flvec = 'GaAs.modes'
!  loto_2d = .true.
  q_in_band_form = .true.
  q_in_cryst_coord = .true.
/
5
0.500 0.500 0.500   20 ! L
0.000 0.000 0.000   20 ! G
0.500 0.000 0.500   20 ! X
0.375 0.375 0.750   20 ! K
0.000 0.000 0.000    1 ! G
mpirun -np 4 matdyn.x -i matdyn.GaAs.in > matdyn.GaAs.out

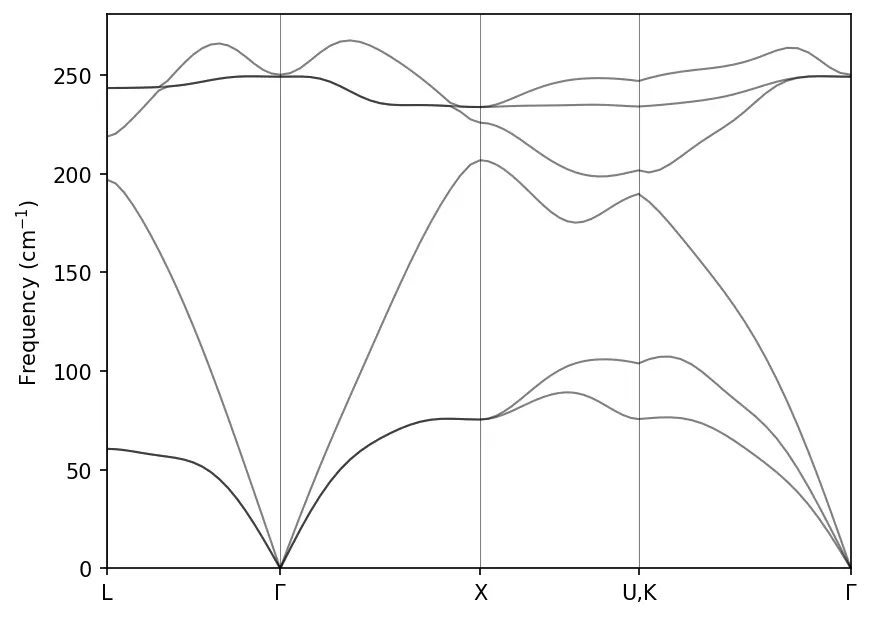
We can now plot the phonon dispersion of GaAs:

notebooks/GaAs-phonon.ipynb
import numpy as np
import matplotlib.pyplot as plt

data = np.loadtxt("../src/GaAs-phonon/GaAs.freq.gp")

nbands = data.shape[1] - 1
for band in range(nbands):
    plt.plot(data[:, 0], data[:, band], linewidth=1, alpha=0.5, color='k')
# High symmetry k-points (check matdyn.GaAs.in)
plt.axvline(x=data[0, 0], linewidth=0.5, color='k', alpha=0.5)
plt.axvline(x=data[20, 0], linewidth=0.5, color='k', alpha=0.5)
plt.axvline(x=data[40, 0], linewidth=0.5, color='k', alpha=0.5)
plt.axvline(x=data[60, 0], linewidth=0.5, color='k', alpha=0.5)
plt.xticks(ticks= [0, data[20, 0], data[40, 0], data[60, 0], data[-1, 0]], \
           labels=['L', '$\Gamma$', 'X', 'U,K', '$\Gamma$'])
plt.ylabel("Frequency (cm$^{-1}$)")
plt.xlim(data[0, 0], data[-1, 0])
plt.ylim(0, )
plt.show()
GaAs-phonon
tip

We may need to lower the value of conv_thr in scf calculation for more accurate result.

Phonon Density of States​

Input file for phonon DOS calculation:

src/GaAs-phonon/matdyn.dos.GaAs.in
&INPUT
  asr   = 'crystal'
  flfrc = 'GaAs.fc'
  flfrq = 'GaAs.dos.freq'
  flvec = 'GaAs.dos.modes'
  dos   = .true.
  fldos = 'GaAs.dos'
  nk1   = 25
  nk2   = 25
  nk3   = 25
/

Plot phonon DOS:

notebooks/GaAs-phonon.ipynb
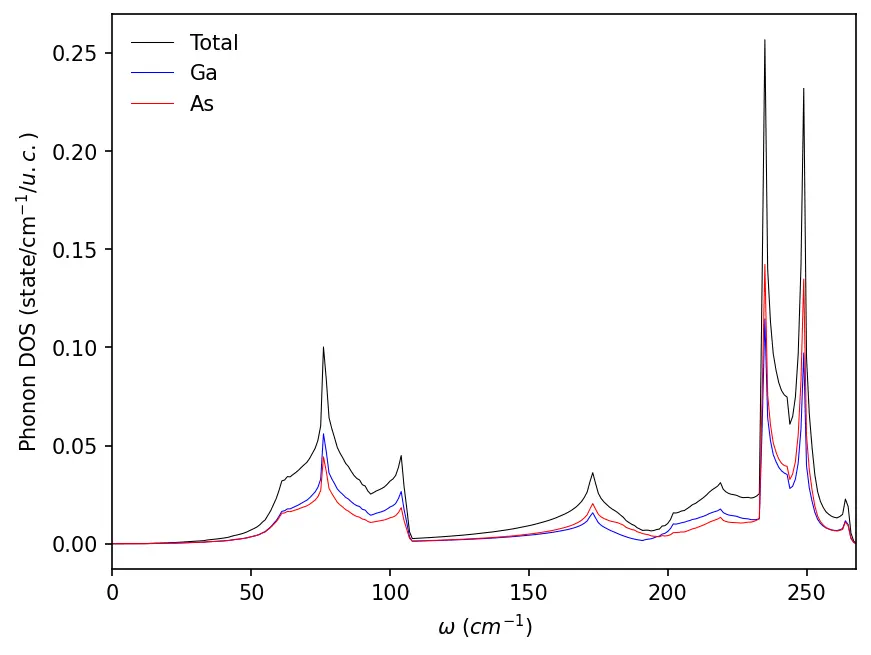
freq, dos, pdos_Ga, pdos_As = np.loadtxt("../src/GaAs-phonon/GaAs.dos", unpack=True)

plt.plot(freq, dos, c='k', lw=0.5, label='Total')
plt.plot(freq, pdos_Ga, c='b', lw=0.5, label='Ga')
plt.plot(freq, pdos_As, c='r', lw=0.5, label='As')
plt.xlabel('$\\Omega~(cm^{-1}$)')
plt.ylabel('Phonon DOS (state/cm$^{-1}/u.c.$)')
plt.legend(frameon=False, loc='upper left')
plt.xlim(freq[0], freq[-1])
plt.show()
GaAs-phonon-dos

Resources​